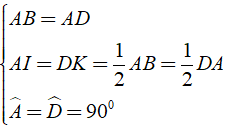Bạn đem bài xích tập dượt minh chứng tứ giác là hình vuông vắn tuy nhiên chúng ta ko biết phương pháp minh chứng như vậy nào? Bởi chúng ta ko ghi nhớ được tín hiệu phân biệt và tính chất hình vuông. Sau phía trên, năng lượng điện máy Ebest tiếp tục share lý thuyết khái niệm hình vuông vắn là gì? Dấu hiệu phân biệt, tính chất hình vuông và cơ hội minh chứng hình vuông vắn cụ thể vô nội dung bài viết sau đây nhằm chúng ta nằm trong tham lam khảo
Hình vuông là gì?
Hình vuông là hình tứ giác đều sở hữu 4 cạnh đều nhau và 4 góc đều nhau (4 góc vuông). cũng có thể coi hình vuông vắn là hình chữ nhật đem những cạnh đều nhau hoặc là hình thoi đem 2 lối chéo cánh đều nhau.
Bạn đang xem: Tính chất hình vuông, dấu hiệu nhận biết, định nghĩa đầy đủ từ A – Z
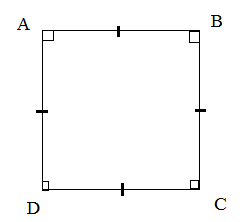
Tính hóa học hình vuông
Trong một hình vuông vắn có:
- Hai lối chéo cánh đều nhau, vuông góc và kí thác nhau bên trên trung điểm của từng lối.
- Có 2 cặp cạnh tuy vậy tuy vậy.
- Có 4 cạnh đều nhau.
- Có một lối tròn trặn nội tiếp và nước ngoài tiếp đôi khi tâm của tất cả hai tuyến đường tròn trặn trùng nhau và là kí thác điểm của hai tuyến đường chéo cánh của hình vuông vắn.
- 1 lối chéo cánh tiếp tục phân tách hình vuông vắn trở thành nhị phần đem diện tích S đều nhau.
- Giao điểm của những lối phân giác, trung tuyến, trung trực đều trùng bên trên một điểm.
- Có toàn bộ đặc thù của hình chữ nhật và hình thoi.
Dấu hiệu phân biệt hình vuông
Một hình tứ giác là một trong hình vuông vắn nếu mà và chỉ nếu mà nó là một trong trong mỗi hình sau:
- Hình chữ nhật đem nhị cạnh kề đều nhau.
- Hình chữ nhật đem hai tuyến đường chéo cánh vuông góc.
- Hình chữ nhật mang 1 lối chéo cánh là phân giác của một góc.
- Hình thoi mang 1 góc vuông.
- Hình thoi đem hai tuyến đường chéo cánh đều nhau.
- Hình bình hành mang 1 góc vuông và nhị cạnh kề đều nhau.
Tham khảo thêm:
- Công thức tính diện tích S hình vuông vắn, chu vi hình vuông vắn chuẩn chỉnh 100%
- Hình thoi là gì? Tính hóa học hình thoi, tín hiệu phân biệt kể từ A – Z
- Tính hóa học hình bình hành, khái niệm, tín hiệu phân biệt kể từ A – Z
Bài tập dượt minh chứng hình vuông
Ví dụ 1: Cho tam giác ABC vuông bên trên A. Phân giác vô AD của góc A (D ∈ BC ). Vẽ DF ⊥ AC, DE ⊥ AB. Chứng minh tứ giác AEDF là hình vuông vắn.
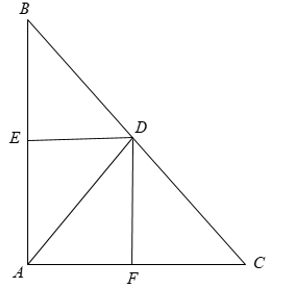
Lời giải
+ Xét tứ giác AEDF đem A∧ = E∧ = F∧ = 900
⇒ AEDF là hình chữ nhật . (1)
Theo fake thiết tao đem AD là lối phân giác của góc Aˆ
⇒ EAD∧ = DAF∧ = 450.
+ Xét Δ AED đem AED∧ = 900; DAE∧ = 450 ⇒ EDA∧ = 450
⇒ Δ AED vuông cân nặng bên trên E nên AE = ED (2)
Từ ( 1 ),( 2 ) ⇒ AEDF là hình vuông
Ví dụ 2: Tìm những hình vuông vắn bên trên hình 105.
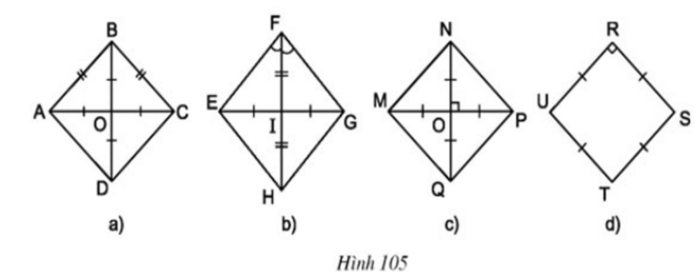
Lời giải
– ABCD đem hai tuyến đường chéo cánh hạn chế nhau bên trên trung điểm từng lối ⇒ ABCD là hình bình hành
Hình bình hành ABCD đem hai tuyến đường chéo cánh đều nhau ⇒ ABCD là hình chữ nhật
Hình chữ nhật ABCD đem AB = BC ⇒ ABCD là hình vuông
– MNPQ đem hai tuyến đường chéo cánh hạn chế nhau bên trên trung điểm từng lối ⇒ MNPQ là hình bình hành
Hình bình hành MNPQ đem hai tuyến đường chéo cánh đều nhau ⇒ MNPQ là hình chữ nhật
Hình chữ nhật MNPQ đem MP ⊥ NQ bên trên O ⇒ MNPQ là hình vuông
– RSTU đem 4 cạnh đều nhau ⇒ RSTU là hình thoi
Hình thoi RSTU mang 1 góc vuông ⇒ RSTU là hình vuông
Ví dụ 3: Cho hình 107, vô cơ ABCD là hình vuông vắn. Chứng minh rằng tứ giác EFGH là hình vuông vắn.
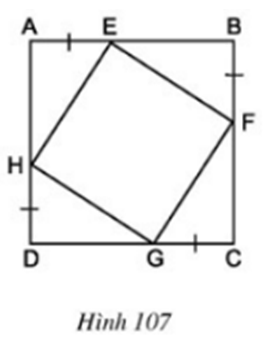
Lời giải:
Do ABCD là hình vuông vắn nên AB = BC = CD = DA.
Theo fake thiết tao có: AE = BF = CG = DH nên tao có:
AB – AE = BC – BF = CD – CG = DA – DH
⇔ BE = CF= DG = HA
Xét những tam giác vuông AEH, BFE, CGF, DHG có:
AE= BF = CG = DH (giả thiết)
HA= BE = CF = DG (chứng minh trên)
⇒ ΔAEH = ΔBFE = ΔCGF = ΔDHG ( c.g.c)
Suy ra: HE = EF = FG = GH (các cạnh tương ứng)

Xem thêm: Giấy xác nhận kiến thức về an toàn thực phẩm có giá trị trong thời hạn bao nhiêu năm (Miễn phí)
Tứ giác EFGH là hình thoi có một góc vày 90o nên EFGH là hình vuông
Ví dụ 4: Cho hình vuông vắn ABCD. Gọi I,K theo lần lượt là trung điểm của AD và DC.
a) Chứng minh rằng BI ⊥ AK.
b) Gọi E là kí thác điểm của BI và AK. Chứng minh rằng CE = AB.
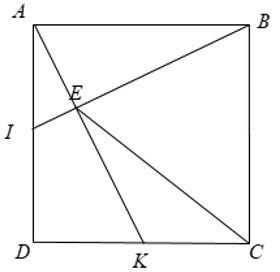
Lời giải
Xét Δ BAI và Δ ADK có:
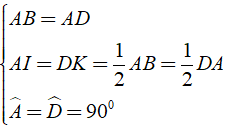
⇒ Δ BAI = Δ ADK (c – g – c)
⇒ ABIˆ = DAKˆ (góc ứng vày nhau)
Mà IAEˆ + EABˆ = 900 ⇒ ABIˆ + EABˆ = 900
+ Xét Δ ABE đem EABˆ + ABEˆ + AEBˆ = 1800
⇒ AEBˆ = 1800 – (ABEˆ + BAEˆ) = 1800 – 900 = 900 hoặc AK ⊥ BI (đpcm)
+ Xét tứ giác EBCK đem KEBˆ + EBCˆ + BCKˆ+ CKEˆ = 3600
⇒ EBCˆ + EKCˆ = 1800.
Mà AKDˆ + AKCˆ = 1800 nên EBCˆ = EKDˆ
+ Tứ giác EBCK nội tiếp nên BECˆ = BKCˆ
Mà BKCˆ = AKDˆ nên EBCˆ = BECˆ hoặc tam giác BEC cân nặng bên trên C
⇒ CE = BC = AB (đpcm)
Ví dụ 5: Cho hình chữ nhật ABCD đem AB = 2AD. Gọi E, F theo dõi trật tự là trung diểm của AB, CD. Gọi M là kí thác điểm của AF và DE, N là kí thác điểm của BF và CE.
a) Tứ giác ADFE là hình gì? Vì sao?
b) Tứ giác EMFN là hình gì? Vì sao?
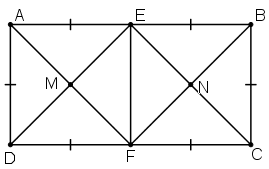
a) E, F là trung điểm AB, CD ⇒ AE = EB = AB/2, DF = FC = CD/2.
Ta có: AB = CD = 2AD = 2BC
⇒ AE = EB = BC = CF = FD = DA.
+ Tứ giác ADFE đem AE // DF, AE = DF
⇒ ADFE là hình bình hành.
Hình bình hành ADFE đem  = 90º
⇒ ADFE là hình chữ nhật.
Hình chữ nhật ADFE là hình chữ nhật đem AE= AD
⇒ ADFE là hình vuông vắn.
b) Tứ giác DEBF đem EB // DF, EB = DF nên là hình bình hành
Do cơ DE // BF
Tương tự: AF // EC
Suy rời khỏi EMFN là hình bình hành
Theo câu a, ADFE là hình vuông vắn nên ME = MF, ME ⊥ MF.
Xem thêm: Vé máy bay Việt Nam
Hình bình hành EMFN đem M̂ = 90º nên là hình chữ nhật.
Lại đem ME = MF nên EMFN là hình vuông vắn.
Bên bên trên đó là toàn cỗ lý thuyết về khái niệm, tín hiệu phân biệt và tính chất hình vuông rất có thể gom chúng ta áp dụng vô thực hiện bài xích tập dượt giản dị và đơn giản nhé