GIỚI THIỆU BÀI HỌC
NỘI DUNG BÀI HỌC
I. Lý thuyết
1. Khoảng cơ hội từ là 1 điểm đến lựa chọn lối thẳng
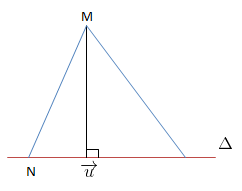
Cho điểm M và lối thẳng \(\Delta\) đi qua quýt N và có một VTCP \(\overrightarrow{u}\)
\(d(M;\Delta )=\frac{\left | \left [ \overrightarrow{NM};\overrightarrow{u} \right ] \right |}{\left | \overrightarrow{u} \right |}\)
\(\left ( =\frac{2S_{\Delta MNP}}{NP} \right )\)
2) Khoảng cơ hội từ nửa đường thẳng liền mạch và mặt mũi bằng phẳng tuy nhiên song
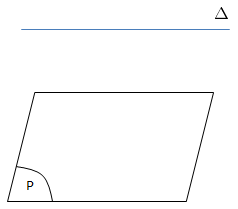
Cho lối thẳng \(\Delta\) và mặt mũi bằng phẳng (P), \(\Delta\) // (P) Ax+By+Cz+D=0, M(x0;y0;z0)
\(d(\Delta;(P))=d(M;(P)) \ \ M \in \Delta\)
\(=\frac{\left | Ax+By+Cz+D \right |}{\sqrt{A^2+B^2+C^2}}\)
3) Khoảng cơ hội thân thuộc hai tuyến đường trực tiếp chéo cánh nhau
Cách 1:
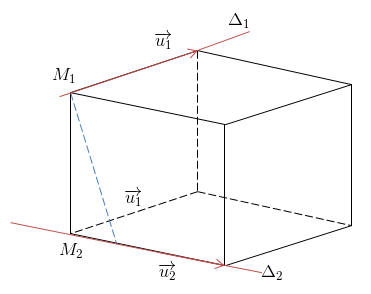
\(\Delta _1\) đi qua quýt M1. có một VTCP \(\overrightarrow{u_1}\)
\(\Delta _2\) đi qua quýt M2. có một VTCP \(\overrightarrow{u_2}\)
\(d(\Delta _1;\Delta _2)=\frac{\left | [\overrightarrow{u_1};\overrightarrow{u_2}] .\overrightarrow{M_1M_2}\right |}{[\overrightarrow{u_1};\overrightarrow{u_2}]}\)

Cách 2:
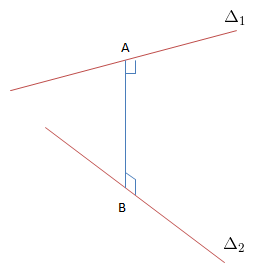
AB là đoạn vuông góc chung \(\Delta _1\), \(\Delta _2\)
\(A\in \Delta _1, B\in \Delta _2\)
\(\Leftrightarrow \left\{\begin{matrix} \overrightarrow{AB}.\overrightarrow{u_1}=0\\ \overrightarrow{AB}.\overrightarrow{u_2}=0 \end{matrix}\right.\)
\(d(\Delta _1;\Delta _2)=AB\)
II. Bài tập
Bạn đang xem: Bài 16: Khoảng cách giữa hai đường thẳng, đường thẳng và mặt phẳng song song
VD1: Cho điểm M(1;2;3) và \(\Delta :\frac{x-1}{2}=\frac{y}{2}=\frac{z+1}{1}\). Tính \(d(M;\Delta )\)
Giải
\(\Delta\) đi qua quýt N(1;0;-1) và có một VTCP \(\overrightarrow{u}=(2;2;1)\)
\(d(M;\Delta )=\frac{\left | [\overrightarrow{NM};\overrightarrow{u}] \right |}{ \left | \overrightarrow{u} \right |}\)
\(\left.\begin{matrix} \overrightarrow{NM}=(0;2;4)\\ \overrightarrow{u}=(2;2;1) \end{matrix}\right\}\)
\([\overrightarrow{NM};\overrightarrow{u}] = \left ( \begin{vmatrix} 2 \ \ 4 \\ 2 \ \ 1 \end{vmatrix}; \begin{vmatrix} 4 \ \ 0 \\ 1 \ \ 2 \end{vmatrix}; \begin{vmatrix} 0 \ \ 2 \\ 2 \ \ 2 \end{vmatrix} \right )=(-6;8;-4)\)
\(d(M;\Delta )=\frac{\left | [\overrightarrow{NM};\overrightarrow{u}] \right |}{ \left | \overrightarrow{u} \right |}= \frac{\sqrt{(-6)^2+8^2+(-4)^2}}{\sqrt{2^2+2^2+1^2}}=\frac{\sqrt{116}}{3} =\frac{2.\sqrt{29}}{3}\)
Cách 2:
\(H\in \Delta \Rightarrow H(1+2t;2t;-1+t)\)
\(\overrightarrow{MH}=(2t;2t-2;-4+t)\)
H là hình chiếu M trên \(\Delta\) nên
\(\overrightarrow{MH}.\overrightarrow{u}=0\Leftrightarrow 4t+2(2t-2)-4+t=0\)
\(\Leftrightarrow 9t=8\Leftrightarrow t=\frac{8}{9}\)
\(\overrightarrow{MH}=(\frac{16}{9};-\frac{2}{9};-\frac{28}{9})\)
\(d(M;\Delta )=MH=\frac{\sqrt{16^2+(-2)^2+(-28)^2}}{9}=\frac{2\sqrt{29}}{3}\)
Nhận xét:
1) Tìm \(H\in \Delta\) sao cho tới MHmin
Xem thêm: Vé máy bay đi Đà Lạt giá rẻ | Vietnam Airlines
VD2: Tìm tọa chừng điểm N nằm trong lối thẳng \(\Delta: \frac{x}{2}=\frac{y}{3}=\frac{z-1}{1}\) và cơ hội d \(\left\{\begin{matrix} x=-1-t\\ y=3+2t\\ z=4+3t \end{matrix}\right.\) một khoảng chừng bằng \(\frac{13\sqrt{42}}{14}\).
Giải
\(N\in \Delta \Rightarrow N(2t;3t;1+t)\)
d trải qua M(-1;3;4), có một VTCP \(\overrightarrow{u}=(-1;2;3)\)
\(\overrightarrow{MN}=(2t+1;3t-3;t-3)\)
\(\overrightarrow{u}=(-1;2;3)\)
\(\left [ \overrightarrow{MN};\overrightarrow{u} \right ]= \left ( \begin{vmatrix} 3t-3 \ \ t-3\\ 2 \ \ \ \ \ \ \ \ \ 3 \end{vmatrix}; \begin{vmatrix} t-3 \ \ 2t+1\\ 3 \ \ \ \ \ \ \ \ \ -1 \end{vmatrix}; \begin{vmatrix} 2t+1 \ \3t-3\\ -1 \ \ \ \ \ \ \ \ \ 2 \end{vmatrix} \right )\)
\(= (7t-3;-7t;7t-1)\)
\(d(N;d)=\frac{\left | [\overrightarrow{MN};\overrightarrow{u}] \right |}{\left | \overrightarrow{u} \right |}=\frac{\sqrt{(7t-3)^2+(-7t)^2+(7t-1)^2}}{\sqrt{(-1)^2+2^2+3^2}}\)
\(=\frac{\sqrt{147t^2-56t+10}}{\sqrt{14}}\)
\(d(N;d)=\frac{13\sqrt{42}}{14}\)
\(\Leftrightarrow \frac{147t^2-56t+10}{14}=\frac{169.42}{14^2}\)
\(\Leftrightarrow 147t^2-56t-497=0\)
\(\Leftrightarrow \Bigg \lbrack\begin{matrix} t=\frac{28-\sqrt{73843}}{147}\\ \\ t=\frac{28+\sqrt{73843}}{147} \end{matrix}\)
\(\Rightarrow N\left ( \frac{56\mp 2\sqrt{73843}}{147}; \frac{84\mp 3\sqrt{73843}}{147} ; \frac{175\mp 2\sqrt{73843}}{147} \right )\)
VD3: Cho lối thẳng \(\Delta \frac{x+1}{-1}=\frac{y-2}{2}=\frac{z}{3}\) và \((P):2x+y+mz-1=0\)
a) Tìm m để \(\Delta //(P)\)
b) Tính \(d(\Delta ;(P))\)
Giải
\(\Delta\) đi qua quýt M(-1;2;0), có một VTCP \(\overrightarrow{u}=(-1;2;3)\)
(P) có một VTPT \(\overrightarrow{n_P}=(2;1;m)\)
a)
\(\Delta\) // (P) \(\Leftrightarrow\left\{\begin{matrix} M\notin (P)\\ \overrightarrow{u}.\overrightarrow{n_P}=0 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} -2+2+0-1\neq 0\\ -2+2+3m=0 \end{matrix}\right.\Leftrightarrow m=0\)
b)
Với m = 0
\((P): 2x+y-1=0\)
\(d(\Delta ;(P))=d(M;(P))=\frac{\left | -2+2-1 \right |}{\sqrt{2^2+1^2}}=\frac{1}{\sqrt{5}}\)
VD4: Cho \((d_1)\left\{\begin{matrix} x=1+2t\\ y=2+t\\ z=-3+3t \end{matrix}\right.(d_2)\left\{\begin{matrix} x=2+u\\ y=-3+2u\\ z=1+3u \end{matrix}\right.\)
a) CMR: d1, d2 chéo cánh nhau
b) Tính d(d1;d2)
Giải
a)
d1 trải qua M1(1;2;-3), có một VTCP \(\overrightarrow{u_1}=(2;1;3)\)
d2 đi qua quýt M2(2;-3;1), có một VTCP \(\overrightarrow{u_2}=(1;2;3)\)
\(\left [ \overrightarrow{u_1};\overrightarrow{u_2} \right ]= \left ( \begin{vmatrix} 1 \ \ 3\\ 2 \ \ 3 \end{vmatrix};\begin{vmatrix} 3 \ \ 2\\ 3 \ \ 1 \end{vmatrix};\begin{vmatrix} 2 \ \ 1\\ 1 \ \ 2 \end{vmatrix} \right )=(-3;-3;3)\)
\(\overrightarrow{M_1M_2}=(1;-5;4)\)
\(\left [ \overrightarrow{u_1};\overrightarrow{u_2} \right ].\overrightarrow{M_1M_2}= -3.1+(-3)(-5)+3.4=24\neq 0\)
Vậy d1, d2 chéo cánh nhau
b)
Cách 1:
\(d(d_1;d_2)=\frac{\left | [\overrightarrow{u_1};\overrightarrow{u_2}.\overrightarrow{M_1M_2 }] \right |}{\left | \overrightarrow{u_1};\overrightarrow{u_2} \right |}= \frac{24}{\sqrt{(-3)^2+(-3)^2+3^2}}=\frac{24}{3\sqrt{3}}=\frac{8}{\sqrt{3}}\)
\(=\frac{8\sqrt{3}}{3}\)
Cách 2:
\(A(1+2t;2+t;-3+3t)\in d_1\)
\(B(2+u;-3+2u;1+3u)\in d_2\)
AB là đoạn vuông góc chung
\(\Leftrightarrow \left\{\begin{matrix} \overrightarrow{AB}.\overrightarrow{u_1}=0\\ \overrightarrow{AB}.\overrightarrow{u_2}=0 \end{matrix}\right.\Rightarrow \left\{\begin{matrix} t\\ u \end{matrix}\right.\)
AB = d(d1;d2)









Bình luận