Tam giác hoặc hay còn gọi là hình tam giác, với 3 điểm, 3 cạnh và 3 góc với tổng số góc vì thế 180o . Hình tam giác được chia nhỏ ra trở thành những loại: Tam giác thông thường, Tam giác cân nặng, Tam giác đều, Tam giác tù, Tam giác vuông, Tam giác vuông cân nặng và Tam giác nhọn.
Để tính được diện tích S, chu vi hình tam giác, bạn phải xác lập được này là loại tam giác gì. Từ cơ mới mẻ dò xét ra sức thức tính đúng đắn. Vậy chào chúng ta nằm trong theo đòi dõi nội dung bài viết tiếp sau đây nhằm làm rõ hơn:
Bạn đang xem: Diện tích tam giác, Chu vi tam giác: Thường, vuông, cân, đều
Phân mô hình tam giác
- Tam giác thường: Là loại tam giác cơ bạn dạng nhất, có tính lâu năm những cạnh không giống nhau, số đo góc vô cũng không giống nhau.
- Tam giác cân: Là tam giác với 2 cạnh, 2 góc cân nhau. Đỉnh của tam giác cân nặng là uỷ thác điểm của 2 cạnh mặt mũi.
- Tam giác đều: Là tam giác với 3 cạnh, 3 góc nhọn cân nhau, là tình huống quan trọng của tam giác cân nặng.
- Tam giác vuông: Là tam giác có một góc vì thế 90°.
- Tam giác tù: Là tam giác với 1 góc vô to hơn 90° hay 1 góc ngoài nhỏ nhiều hơn 90 (một góc nhọn).
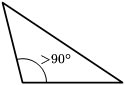
- Tam giác nhọn: Là tam giác với 3 góc vô đều nhỏ rộng lớn 90° hoặc với toàn bộ góc ngoài to hơn 90°.
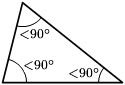
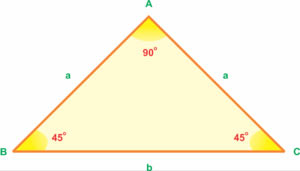
- Tam giác vuông cân: Vừa là tam giác vuông, vừa phải là tam giác cân nặng. Có 2 cạnh góc vuông cân nhau và từng góc nhọn vì thế 45°.
Công thức Tính diện tích S tam giác
Diện tích tam giác thường
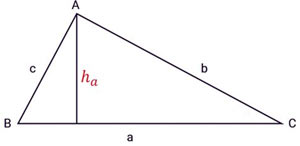
Tam giác ABC với 3 cạnh a, b, c, ha là lối cao kể từ đỉnh A. Các công thức tính diện tích S tam giác thường:
Công thức chung:
Diện tích tam giác vì thế ½ tích của độ cao hạ kể từ đỉnh với chừng lâu năm cạnh đối lập của đỉnh đó:

Khi biết một góc:
Diện tích tam giác vì thế ½ tích 2 cạnh và sin của góc ăn ý vì thế 2 cạnh đó:

Sử dụng công thức Heron:

Trong cơ p là nửa chu vi tam giác:

Vậy công thức tiếp tục là:

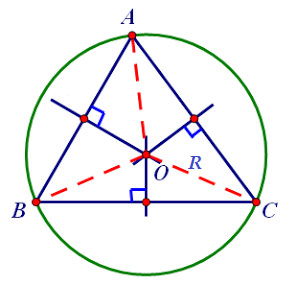
Với R là nửa đường kính lối tròn trĩnh nước ngoài tiếp tam giác:

Cách khác: 
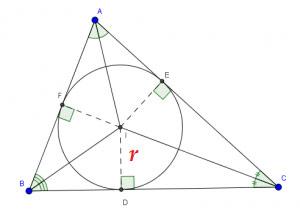
Với r là nửa đường kính lối tròn trĩnh nội tiếp tam giác:

Diện tích tam giác đều
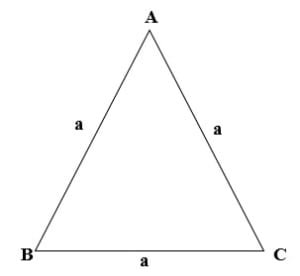
Tam giác đều ABC với 3 cạnh cân nhau, vô cơ a là chừng lâu năm những cạnh của tam giác, nên đơn giản vận dụng toan lý Heron nhằm suy ra:

Diện tích tam giác cân
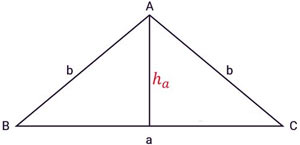
Diện tích tam giác cân đối tích độ cao nối kể từ đỉnh tam giác cơ cho tới cạnh lòng tam giác, rồi phân chia cho tới 2. Trong số đó, a là chừng lâu năm cạnh lòng, độ cao là ha:

Diện tích tam giác vuông
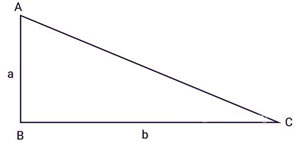
Tam giác vuông ABC, có tính lâu năm 2 cạnh góc vuông theo lần lượt là a, b. Công thức tính diện tích S tam giác vuông là:

Diện tích tam giác vuông cân
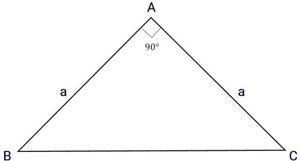
Tam giác ABC, vuông cân nặng bên trên A, a là chừng lâu năm 2 cạnh góc vuông:
Xem thêm: Cơ cấu giải thưởng xổ số truyền thống Miền Nam. - Xổ số Minh Ngọc™

Công thức Tính chu vi tam giác
Chu vi tam giác thường
Công thức tính chu vi hình tam giác thông thường vì thế chừng lâu năm tổng 3 cạnh của tam giác đó:

Trong đó:
- P là chu vi tam giác.
- a, b, c là 3 cạnh của hình tam giác cơ.
Theo cơ, nếu còn muốn tính diện tích S nửa chu vi tam giác tiếp tục dựa vào công thức:

Chu vi tam giác vuông
Công thức tính chu vi tam giác vuông:

Trong đó:
- a và b: Hai cạnh của tam giác vuông
- c: Cạnh huyền của tam giác vuông.
Chu vi tam giác cân
Tam giác cân nặng là tam giác với 2 cạnh mặt mũi cân nhau, nên công thức tính chu vi tam giác cân nặng tiếp tục như sau:

Trong đó:
- a: Hai cạnh mặt mũi của tam giác cân nặng.
- c: Là lòng của tam giác.
Lưu ý: Công thức tính chu vi tam giác cân nặng cũng khá được vận dụng nhằm tính chu vi của tam giác vuông cân nặng.
Chu vi tam giác đều
Tam giác đều là tam giác với 3 cạnh cân nhau, vậy công thức tính chu vi tam giác đều tiếp tục là:

Trong đó:
- P: Là chu vi tam giác đều.
- a: Là chiều lâu năm cạnh của tam giác.
8 công thức tính diện tích S tam giác nâng cao
Cho tam giác ABC, tao kí hiệu chừng lâu năm những cạnh là a=BC, b=CA, c=AB, những góc của tam giác được viết lách giản dị và đơn giản là A,B,C. Diện tích tam giác được kí hiệu là S.
Công thức 1
Gọi chừng lâu năm lối cao (chiều cao) hạ kể từ những đỉnh A,B,C theo lần lượt là ha, hb, hc.

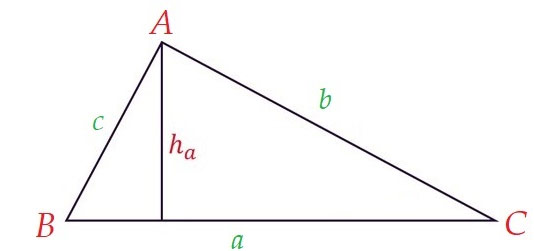
Đặc biệt:
Diện tích tam giác vuông bên trên A là: 
Diện tích tam giác cân nặng bên trên A là:  (với H là trung điểm của BC).
(với H là trung điểm của BC).
Diện tích tam giác đều cạnh a là: 
Công thức 2

Công thức 3
Gọi R là nửa đường kính lối tròn trĩnh nước ngoài tiếp tam giác ABC. Ta có: 
Công thức 4
Gọi r là nửa đường kính lối tròn trĩnh nội tiếp tam giác ABC và p là nửa chu vi tam giác ( ):
): 
Công thức 5 (Công thức Héron)
Với p là kí hiệu nửa chu vi như ở mục 4, tao có: 
Xem thêm: kqxsmb, xsmt, xsmn, xo so 3 mien nhanh nhat
Công thức 6

Công thức 7
Trong mặt mũi phẳng lì Oxy, gọi tọa chừng những đỉnh của tam giác ABC là: A(xA,yA),B(xB,yB),C(xC,yC).
Khi đó: 
Công thức 8
Áp dụng vô không khí, với định nghĩa tích với vị trí hướng của 2 vectơ. Ta có: ![S=\frac{1}{2} |[\underset{AB}{\rightarrow} ,\underset{AC}{\rightarrow} ]|](https://o.rada.vn/data/image/holder.png)














