Lý thuyết Hệ thức Vi-ét và ứng dụng.

1. Các kiến thức và kỹ năng cần thiết nhớ

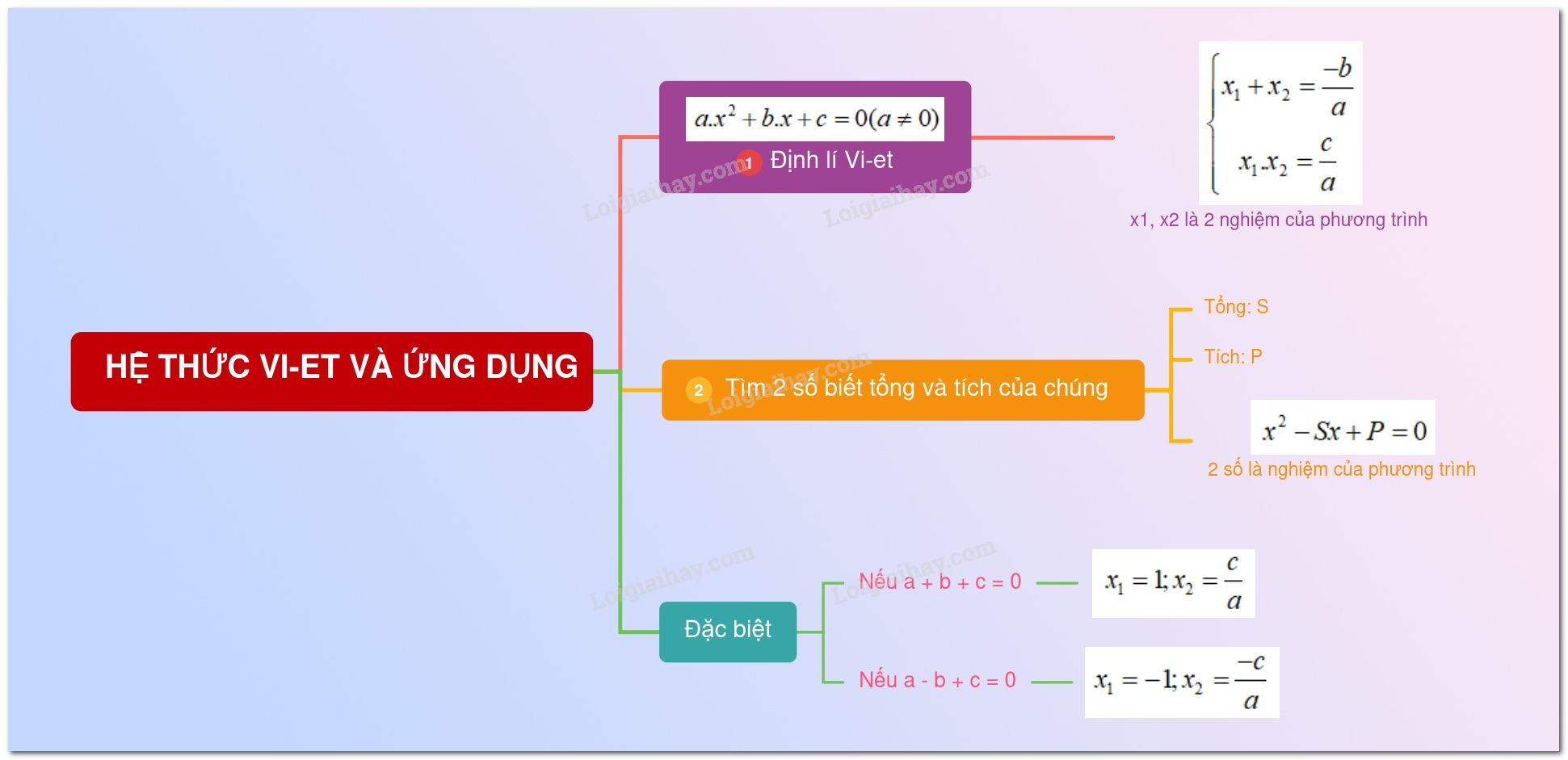
Hệ thức Vi-ét

Bạn đang xem: Lý thuyết Hệ thức Vi-ét và ứng dụng. | SGK Toán lớp 9

Cho phương trình bậc nhị $a{x^2} + bx + c = 0\,(a \ne 0).$
Nếu ${x_1},{x_2}$ là nhị nghiệm của phương trình thì $\left\{ \begin{array}{l}{x_1} + {x_2} = \dfrac{{ - b}}{a}\\{x_1} \cdot {x_2} = \dfrac{c}{a}\end{array} \right..$

Ví dụ: Phương trình $2x^2-5x+2=0$ với $ \Delta=9>0$ nên phương trình với nhị nghiệm $x_1;x_2$.

Theo hệ thức Vi-ét tao có: $\left\{ \begin{array}{l}{x_1} + {x_2} = \dfrac{{ 5}}{2}\\{x_1} \cdot {x_2} = \dfrac{2}{2}=1\end{array} \right..$

Ứng dụng của hệ thức Vi-ét

+) Xét phương trình bậc hai: $a{x^2} + bx + c = 0\,(a \ne 0).$

Nếu phương trình với $a + b + c = 0$ thì phương trình với cùng một nghiệm là ${x_1} = 1,$ nghiệm ê là ${x_2} = \dfrac{c}{a}.$

Nếu phương trình với $a - b + c = 0$ thì phương trình với cùng một nghiệm là ${x_1} = - 1,$ nghiệm ê là ${x_2} = - \dfrac{c}{a}.$

+) Tìm nhị số biết tổng và tích của chúng : Nếu nhị số với tổng vì chưng $S$ và tích vì chưng $P$ thì nhị số này là nhị nghiệm của phương trình ${X^2} - SX + Phường = 0$ (ĐK: ${S^2} \ge 4P$)

Ví dụ:

+ Phương trình $2x^2-9x+7=0$ với $a+b+c=2+(-9)+7=0$ nên với nhị nghiệm $x_1=1;x_2=\dfrac{c}{a}=\dfrac{7}{2}$

+ Phương trình $2x^2+9x+7=0$ với $a-b+c=2-9+7=0$ nên với nhị nghiệm $x_1=-1;x_2=-\dfrac{c}{a}=-\dfrac{7}{2}$

2. Các dạng toán thông thường bắt gặp

Dạng 1: Không giải phương trình, tính độ quý hiếm biểu thức tương quan trong những nghiệm.

Phương pháp:

Bước 1 : Tìm ĐK nhằm phương trình với nghiệm : $\left\{ \begin{array}{l}a \ne 0\\\Delta \ge 0\end{array} \right.$. Từ ê vận dụng hệ thức Vi-ét tao có : $S = {x_1} + {x_2} = - \dfrac{b}{a}$ và $P = {x_1}{x_2} = \dfrac{c}{a}$.

Bước 2 : Biến thay đổi biểu thức đối xứng trong những nghiệm của đề bài xích theo gót tổng ${x_1} + {x_2}$ và tích ${x_1}{x_2}$, tiếp sau đó vận dụng bước 1.

Một số biểu thức đối xứng trong những nghiệm thông thường bắt gặp là :

+) $A = x_1^2 + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2}= {S^2} - 2P$

+) $B = x_1^3 + x_2^3$

$= {\left( {{x_1} + {x_2}} \right)^3} - 3{x_1}{x_2}\left( {{x_1} + {x_2}} \right)= {S^3} - 3SP$

+) $C = x_1^4 + x_2^4 = {\left( {x_1^2 + x_2^2} \right)^2} - 2x_1^2x_2^2$

$= {\left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - 2{x_1}{x_2}} \right]^2} - 2{\left( {{x_1}{x_2}} \right)^2}= {\left( {{S^2} - 2P} \right)^2} - 2{P^2}$

+) $D = \left| {{x_1} - {x_2}} \right| $

$= \sqrt {{{\left( {{x_1} + {x_2}} \right)}^2} - 4{x_1}{x_2}} $.

$E = {\left( {{x_1} - {x_2}} \right)^2} = {\left( {{x_1} + {x_2}} \right)^2} - 4{x_1}{x_2}$

Xem thêm: Vietnam Visa for Saudi Arabia Citizens - Vietnam evisa up to 90 days 2024

$= {S^2} - 4P $.

Dạng 2 : Giải phương trình bằng phương pháp nhẩm nghiệm

Phương pháp :

Xét phương trình bậc hai : $a{x^2} + bx + c = 0{\rm{ }}\left( {a \ne 0} \right)$.

+) Nếu phương trình với $a + b + c = 0$ thì phương trình với cùng một nghiệm ${x_1} = 1$, nghiệm ê là ${x_2} = \dfrac{c}{a}.$

+ ) Nếu phương trình với $a - b + c = 0$ thì phương trình với cùng một nghiệm ${x_1} = - 1$, nghiệm ê là ${x_2} = - \dfrac{c}{a}.$

+) Nếu ${x_1},{x_2}$ là nhị nghiệm của phương trình thì $\left\{ \begin{array}{l}S = {x_1} + {x_2} = - \dfrac{b}{a}\\P = {x_1}{x_2} = \dfrac{c}{a}\end{array} \right.$.

Dạng 3 : Phân tích tam thức bậc nhị trở thành nhân tử

Phương pháp :

Nếu tam thức bậc nhị $a{x^2} + bx + c{\rm{ }}\left( {a \ne 0} \right)$ với nhị nghiệm ${x_1}$ và ${x_2}$ thì nó được phân tách trở thành nhân tử: $a{x^2} + bx + c = a\left( {x - {x_1}} \right)\left( {x - {x_2}} \right)$.

Dạng 4 : Tìm nhị số lúc biết tổng và tích

Phương pháp :

Để lần nhị số $x,y$ lúc biết tổng $S = x + y$ và tích $P = xy$, tao thực hiện như sau:

Bước 1: Xét ĐK ${S^2} \ge 4P$. Giải phương trình ${X^2} - SX + Phường = 0$ nhằm lần những nghiệm ${X_1},{X_2}$.

Bước 2: Khi ê những số cần thiết lần $x,y$ là $x = {X_1},hắn = {X_2}$ hoặc $x = {X_2},hắn = {X_1}$.

Dạng 5 : Bài toán tương quan cho tới lốt những nghiệm của phương trình bậc hai

Phương pháp :

Xét phương trình $a{x^2} + bx + c = 0\left( {a \ne 0} \right)$. Khi đó:

1. Phương trình với nhị nghiệm ngược lốt $ \Leftrightarrow ac < 0$.

2. Phương trình với nhị nghiệm phân biệt nằm trong lốt $ \Leftrightarrow \left\{ \begin{array}{l}\Delta > 0\\P > 0\end{array} \right.$.

3. Phương trình với nhị nghiệm dương phân biệt $ \Leftrightarrow \left\{ \begin{array}{l}\Delta > 0\\P > 0\\S > 0\end{array} \right.$.

4. Phương trình với nhị nghiệm âm phân biệt $ \Leftrightarrow \left\{ \begin{array}{l}\Delta > 0\\P > 0\\S < 0\end{array} \right.$.

5. Phương trình với nhị nghiệm ngược lốt nhưng mà nghiệm âm có mức giá trị vô cùng to hơn nghiệm dương $ \Leftrightarrow \left\{ \begin{array}{l}ac < 0\\S < 0\end{array} \right.$.

Dạng 6 : Xác lăm le ĐK của thông số nhằm nghiệm của phương trình vừa lòng ĐK cho tới trước.

Phương pháp :

Bước 1. Tìm ĐK nhằm phương trình với nghiệm $\left\{ \begin{array}{l}a \ne 0\\\Delta \ge 0\end{array} \right.$.

Xem thêm: CTY TNHH DU LỊCH BAY VIỆT MỸ | VIET MY GROUP

Bước 2. Từ hệ thức vẫn cho tới và hệ thức Vi-ét, tìm kiếm ra ĐK của thông số.

Bước 3. Kiểm tra ĐK của thông số coi với vừa lòng ĐK ở bước 1 hay là không rồi Tóm lại.